Algorithms : Backtracking

June 5, 2025 5 분 소요

이번 포스트에서는 Backtracking 이라는 알고리즘에 대해 설명한다. 그리고 Backtracking의 여러 예제와 마지막 0/1 Knapsack 을 이 알고리즘으로 풀어본다.

Greedy VS Dynamic Programming

왜 Greedy 알고리즘이 중요한가?

Heuristic기반 (경험지식에서 가져온다.)
간단하고, 빠르고, 구현에 용이하다.
새로운 문제의 baseline 전략으로 유용하다.
Optimal한 Substructure가 있다면 global Optimal도 가능하다.
- 물론 증명은 필요하다.

Knapsack Problem

문제 정의

Input : 아이템 n개가 있고, 각 아이템마다 Weight 와 Profit이 존재한다. W로 총 용량도 존재한다.
Goal : weight의 총합이 W보다 작음을 만족하면서 Profit을 최대화하는 Subset A를 찾아라
응용 예시
- 도둑 가방 문제
- 스타트업 투자 문제 (투자금의 제약 -> 최적이 아이템 조합 )
해결 방법 비교

Brute Force (BF) : 모든 경우를 탐색한다. 성능은 매우 느리다. \(O(2^n)\)
Divide & Conquer : Optimal을 찾을 수는 있지만, 효율적이지 않다.
Dynamic Programming : Optimal을 보장한다. \(O(nW)\)
Greedy : 빠르다, 일부 경우에만 Optimal 하다. (Fractional 가능)
- 0/1 Knapsack에서는 Optimal 하지 않다.

Greedy idea 접근

Profit 기준으로 정렬

Profit이 높은 item 부터 넣는다.
KnapSack 용량이 초과될 수도 있다. -> 그렇기에 profit 기준으로만 넣는다고 할 때 반례가 생긴다.

Profit per Unit Weitght 기준 정렬

각 아이템의 가치 / 무게 비율을 기준으로 정렬해서 넣는다.
Fractional Knapsack과 같이 쪼개서 넣는 경우가 가능할 때는 이 방법이 가장 효율이 높다.
하지만, 어떤 경우에도 비율이 낮은 아이템을 하나만 넣는 것 전체 profit 보다 클 수 있다.
- 따라서 0/1 Knapsack에서는 DP를 사용해야 Optimal을 보장할 수 있다.

DP Design

Knapsack 문제는 Optimal Substructure와 Overlapping Subproblem을 만족한다.

1D Array에서는 실패한다.

weight 조건을 고려하지 못해서 단순히 아이템을 몇개까지 선택했는가 만을 가지고서는 최적해를 만들 수 없다.
따라서 2차원 배열이 필요하다.

2D Array

1차원 : Item Index (몇 번째 아이템까지 고려했는가?)
2차원 : Weight (현재까지의 총 무게가 얼마인가?)

DP Table

p[i , w] = item 1 ~ i 까지 고려했을 때, 총 weight <= W인 경우 얻을 수 있는 최대 profit
Recurrence Relation \(p[i, w] = \max \Big( p[i-1, w],\ p[i-1, w - w_i] + p_i \Big)\)
해석 : 두 가지 경우 중에 더 좋은 것을 선택한다.
- Item i를 넣지 않은 경우 : 이전 결과를 그대로 사용한다.
- Item i를 넣는 경우 : 이전의 용량으로 만들었던 best 결과에 Profit을 추가한다.

DP Anlaysis

Time Complexity

DP에서 사용한 table은 p[i,w] 인 2차원 테이블이다.
즉 table의 크기는 n X W 이다.
전체 시간복잡도 \(O(n \times W)\)
Space Complexity
- 기본적으로 n X W 공간이 필요하다.
- 최적화하면 O (W) 공간으로 줄일 수 있다.

Pseudo - Polynomial Time

입력 크기 n은 item의 개수
W는 입력이 아니라 숫자 값이다.
W가 너무 큰 수가 나와버리면 시간 복잡도가 실질적으로 매우 커진다.

DP Optimization Idea

모든 p[i,w]를 반드시 계산할 필요는 없다.

현재 남은 weight가 w < w_i 인 경우에는 Item_i를 넣을 필요가 없다.

즉, 일부 경우에는 row마다 현재 가능한 weight 구간만 계산하도록 최적화가 가능하다.

문제 본질이 Hard (NP - Hard) 부분에 속한다.

-> 따라서 더 큰 Scale의 문제를 풀기 위해서는 새로운 Algorithm이 필요하다.

DFS VS BFS

DFS

깊이 우선 탐색 : 한 방향으로 끝까지 파고 들어간다.
자료구조는 Stack을 사용한다.
방문 순서 : 루트 -> 자식 -> 자식의 자식 ->… (끝까지) -> 백트래킹

BFS

너비 우선 탐색 : 가까운 노드부터 차례로 탐색한다.
자료구조로는 Queue를 사용한다.
방문순서 : 루트 -> 루트의 인접 노드 전부 -> 다음 레벨 인접노드 -> ….

Backtracking

Backtracking = “체계적인 Brute-Force”
모든 경우의 수를 다 보는 것처럼 보이지만, 불피요한 가지를 조기에 잘라내는 전략이다.
이론보다는 실제적인 속도를 줄인다.
- Brute-Force : 모든 조합과 경로를 탐색
- Backtracking : 가능한 경우만 탐색하고, 가능하지 않아보이면 가지치기를 한다. (Pruning)
구현 방법 : 보통 DFS 기반 (재귀를 사용한다.)

DFS로 탐색을 진행
Promising Check 이후에 유망하면 계속 진행한다.
Non-Promising 이면 backtracking 한다.
State-Space Tree로 구성한다.

Backtracking : N-Queen

N X N 체스판에 N개의 Queen을 배치한다.
단, 서로 공격하지 않게 배치해야 한다.

Search Tree 구성

각 레벨 = Queen을 한 행(row)에 하나씩 놓는 과정
Promising check:
- 같은 행이면 안된다.
- 같은 열이면 안된다.
- 같은 대각선에 있어도 안된다.
시간 복잡도 : (4-Queen) 일때를 가정 \(16^n\)
- 실제로는 Pruning으로 훨씬 짧아진다.

Backtracking : Subset Sum

Items의 부분집합들을 고른다.
고른 Item의 weight의 총 합은 W 가 되야 한다.
0/1 Knapsack 문제에서의 Special Case
구현 방법
- Brute- Force : 모든 부분 집합을 다 세는 경우 \(O(2^n)\)
- Backtracking : 사용 시 promising check를 통해 pruning
Promising check

Non- Promising 조건 (이 2가지 제외하고는 다 성립)

weight 에서 다음 item의 weight를 더하니 전체 W보다 크다
weight 에서 남은 item의 total weight를 더해도 전체 W보다 작다.

item들이 역순 또는 random으로 정렬되어 있다면.?

정렬한게 우수한 경우
- 중복 제거에 효율적이다.
  - 정렬을 하지 않으면 path 전체와 result 전체를 비교해야한다.
  - 정렬하면 한줄로 중복을 방지할 수 있어 빠르다
- 문제 요구가 많은 경우에 효율적이다.
  - 중복 없이 출력, 사전순으로 출력과 같이 조건이 많아지면 정렬이 필수이다.
  - 정렬 후에 탐색하면 더 코드가 깔끔해지고 단순해진다.
정렬 안하는게 우수한 경우
- 순서 그대로 subset을 구성할 때
  - 어떠한 경우에는 원래 배열의 순서를 보존해야하는 경우도 있는데 이 때는 정렬을 안하는게 맞다.
  - 정렬에는 O(N log N)의 시간이 소요된다. 즉, 큰 데이터에서는 정렬없이 진행해야 더 빠른 경우도 존재한다.
- 사실 상 모든 부분집합을 출력하는 것에 있어서 순서는 무관하다.

Backtracking : Graph Coloring

무방향 그래프를 m 개의 색으로 칠한다.
인접한 노드는 다른 색이여야 한다.
적용 예시 ) 무선 네트워크, 자원 할당 문제
구현 방법
- DFS 기반 Backtracking
- promising check : 현재 node를 색칠 할 때 인접한 노드에 같은 색이 없는지 확인한다.
- 시간 복잡도 \(O(m^n)\)

이 예제에서 생각할 수 있는 질문

Q1) 최소의 m을 어떻게 찾을 수 있는가?

Q2) 주어진 m으로 m이 colorable 여부를 확인할 수 있는가?

Efficient poly alg 이 없다.

이 그래프를 coloring 하기 위해 최소 몇 개의 색이 필요한지를 찾는 문제는 NP - Hard문제이다.
- 효율적인 다항시간 알고리즘(poly-time alg)은 존재하지 않는다.
최소의 m을 구하는 것은 매우 어려운 문제이고 보통 정확하게 풀기 위해서는 exponential한 탐색이 필요하다
m을 1부터 시작해서 하나씩 늘려가며 m-colorable 여부를 확인하는 접근이 필요하다.

반면에 주어진 m 이 있을 때는 colorable 할 수 있는지는 Backtracking을 활용하여 찾을 수 있다.

정점에 하나씩 색을 배정해가며, 현재까지의 색이 유효한지 체크한다.
이 경우는 탐색 공간이 m^n이지만, pruning이 가능하므로 실제로 많은 경우 빠르게 판단이 가능하다.

Backtracking : Hamiltonian Cricuit

HC : Hamiltonian Circuit
모든 vertex를 정확히 1번씩 방문한 후에, 다시 출발점으로 돌아오는 경로를 찾아라
Promising check
- i-th node는 vaild한 node인지 확인한다.
- 마지막 node는 출발 node로 돌아갈 수 있어야한다.
- 방문한 node의 중복은 안된다.
DFS 기반으로 promising check 하면서 State-space Tree 생성
시간복잡도 \(Brute Force : O(n!)\)
- 모든 경로를 다 탐색하는 경우
- Backtracking을 사용하면 전체 n!중에서 불가능한 가지를 pruning한다. 따라서 시간이 절약된다.

KnapSack을 하기 전의 예제를 보면서 확인할 수 있는 결론들

Backtracking = 똑똑한 Brute-Force
가장 중요한 건 promising function 설계
- 잘 설계할수록 pruning 효과가 커짐 → 실행 속도 비약적 향상
DFS 기반으로 구현
다양한 NP-hard 문제에 활용 가능

Backtracking : 0/1 Knapsack

KnapSack 문제 다시 정리

W 무게 이하로 item을 넣어서 Profit을 최대화한다.
Promising Function
- 탐색 중 현재 branch가 promising 한지 판단한다.
- 유망하지 않으면 pruning 한다.
Non-Promising Check

현재까지 weight가 W 초과 -> Stop
앞으로 추가 가능한 item weight 합쳐도 W 초과 -> Stop

Bounding Function

현재까지 profit + 앞으로 최대로 얻을 수 있는 profit 추정 -> Bound 계산
Bound < Best -> 더 이상 볼 필요가 없다. (Pruning)

Bound 구성

g = 현재까지 얻은 profit
h = 앞으로 얻을 수 있는 최대 profit 추정
- 예 : 남은 item 중 fraction까지 고려한 greedy 한 추정 값 사용
Bound = g + h
문제를 전개해보면 아래와 같다.

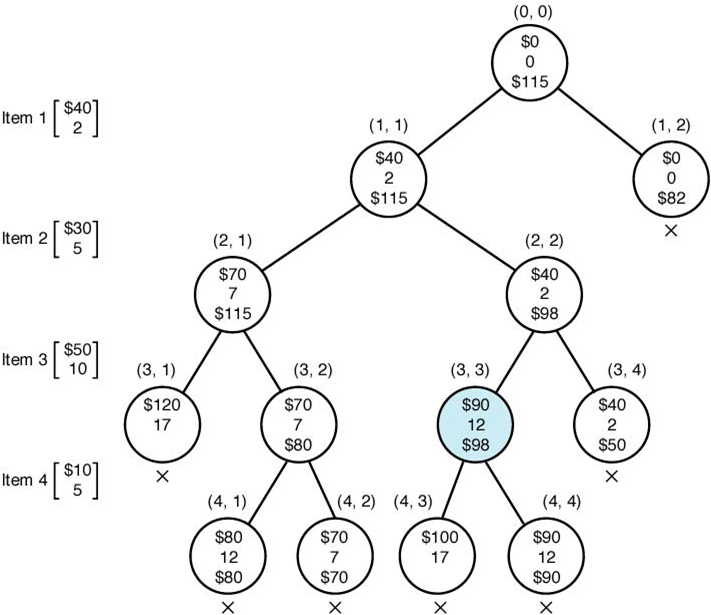
0-1_knapsack_dfs

Bounding Function 이란?

Bounding Function

현재 노드에서 앞으로 최대로 얻을 수 있는 profit을 계산해서 Bound의 값을 만들어낸다. \(Bound = 현재 profit + 앞으로가능한 최대 profit\)
- 얼마나 더 좋은 해를 기대할 수 있는가
- Upper Bound
Non-promising function
- 현재 노드가 탐색할 가치가 있는지 여부를 판단하는 Function
- 판단의 기준 중 하나로 Bounding Function 값을 사용한다.

Twitter Facebook LinkedIn