Compiler - Syntax Analysis(03)

이번에는 Syntax Analysis의 Bottom-up Parsing과 Shift-reduce parsing과 LR(0)과 SLR(1)에 대해 테이블을 만들어보고 마지막으로 AST(Abstract Syntax Tree)까지 다룬다.

Syntax Analysis (Part 3)

---

Bottom-Up Parsing

Parse trees가 bottom up to the top (leaves -> root)

(장점)

Top-Down LL(1) 문법만 처리가 가능 (제약이 많음)

• Bottom-Up 은 LR, LALR, SLR 등 더 많은 문법을 처리 가능

-> 즉, left-recursive, ambiguous한 문법도 처리가 가능함.

• 모호성 제거에 유리

-> shift/reduce , reduce/reduce conflict 명시적 해결이 가능

-> 따라서 우선 순위와 결합 규칙을 명확히 적용 가능함.

(단점)

• 구현 복잡도가 더 높음

Shift-Reduce Parsing

LR Parsing

• L : Left-to-Right scanning of input
• R : Rightmost derivation

Shift-Reduce Parsing의 개념

입력 문자열을 오른쪽에서 왼쪽으로 줄여 나가며 최종적으로 시작 기호 S 하나로 만드는 방식

• 입력 문자열을 Shift(이동) 또는 Reduce(축소) 하며 파싱을 진행
• Rightmost Derivation in Reverse를 따름
• 입력을 왼쪽부터 읽고, 우측 유도 과정을 역순으로 수행

핵심 Key idea

Splitter

• 파서가 입력 스트링을 둘로 나누는 지점
• 이 지점을 기준으로 왼쪽은 지금까지 처리한 부분(stack), 오른쪽은 아직 남은 입력
• 파서가 매번 shift / reduce를 결정

| 기호를 사용 => Union이랑 헷갈리지 말 것

Left Substring

• 지금까지 Shift된 부분 문자열
• 파싱 스택에 쌓인 심볼들로 이 부분에서 규칙을 찾아 Reduce를 할 수 있음.

Right Substring

• 아직 읽지 않은 입력 (a sequence of terminal)
• 아직 Shift 되지 않은 심볼들의 나머지 부분으로 파서는 이 부분을 읽으며 계속 스택을 채워 나감.

Shift - Reduce 작동 방식

작업	설명
Shift	입력 토큰을 스택으로 이동
Reduce	스택 상단의 문자열이 production RHS와 일치할 경우, 이를 LHS로 치환

Conflict

• Shift/Reduce Conflict

파서가 어떤 시점에서 Shift or Reduce를 해야 할지 결정하지 못할 때 발생하는 충돌

지금 줄일까? 아니면 더 읽을까? 를 결정하지 못해서 충돌이 생김.

예시)

stmt → if expr then stmt

if expr then stmt else stmt

Input : if E1 then if E2 then S1 else S2

​ 두 가지의 가능한 해석

1. Reduce

   먼저 if E2 then S1 을 하나의 stmt로 보고

   → if E1 then stmt 로 reduce 하려는 경우

2. Shift

   아직 else가 남아 있으니

   → 더 많은 토큰을 읽기 위해 shift 하려는 경우

• Reduce / Reduce Conflict

두 개 이상의 production을 동시에 reduce할 수 있을 때 발생하는 충돌로 파서가 여기서 어떤 규칙을 사용해 줄여야하는지 둘 이상의 후보로 두고 결정을 하지 못하고 있는 상황

예시)

A → α
B → α S → A | B

Input 이 α 일 때, A로 줄일지, B로 줄일지 파서가 결정을 못하는 상황

=> 둘 다 reduce가 가능하기에 conflict 발생

Handle & Viable Prefix

어떻게 Shift or Reduce를 결정해야할까?

Reduce를 해도 그 결과가 결국 시작 기호(Start Symbol)로 줄여질 수 있을 때만 Reduce를 해야한다

Handle

현재 파싱 문자열에서 하나의 production rule을 적용하여 줄일 수 있는 우변 부분을 의미함.

현재 줄일 수 있는 RHS에 완전히 일치하는 부분 문자열

Handle = 우변(β)의 instance

즉, 파싱 중인 문자열에서 한 번의 reduce로 좌변(A)으로 바뀔 수 있는 부분

• Bottom-up parser는 항상 Handle을 찾아서 reduce함.
• LR Parser가 정확히 Handle의 위치를 결정해주는 알고리즘

(특징)

Handle은 항상 Stack의 Top에 있다.

• Shift-Reduce 방식은 입력을 오른쪽에서 왼쪽으로 파싱하는 과정
• 그래서 제일 최근에 만들어진 것(=handle)은 항상 Stack의 위쪽에 존재하게 됨. => 편리한 성질
  • 따라서 Unambiguous CFG일때, Shift-Reduce Parser는 handle에서만 reduce 해야함.

요약 : Handle = 줄일 준비가 된 부분

파서 입장에서 ‘여기서 줄여도 괜찮을까’에 대한 판단 기준

Viable Prefix

핸들을 포함하거나, 핸들 바로 앞까지만 포함하는 접두사

Left Substring that can appear during shif-reduce parsing of an acceptable input string

• Shift-Reduce Parsing 도중에 올 수 있는 ** “정당한” 입력 문자열의 왼쪽 부분 문자열로 **핸들이 오기 전까지 또는 **핸들을 막 포함한 시점까지의 ** 모든 중간 결과들을 말함.

더 완성된 문장임을 알기 위해 더 읽어보고 완성된 문장인지 판단하는 것과 같음.

예시)

상태	판단 기준	이유
F | * id	Shift
F * | id	Shift
F * id |	Reduce (id → F)

F는 T-> F 로 reduce 할 수 있는 핸들처럼 보이지만, 그 다음에 * 가 오고 있기 때문에 지금은 아직 핸들이 아님

=> 파서가 충분한 정보를 얻기 전까지는 Shift를 계속 수행하고, 핸들이 확실해지면 그 때 Reduce를 하는 방식으로 수행.

• Viable Prefix를 인식하는 방법

Viable Prefix는 여러 개의 생성 규칙 오른쪽 (RHS) 의 접두사들이 붙어서 생긴 형태라는 것

정확한 기준

어떤 Viable Prefix가 어떤 production의 RHS의 전체(완전한 우변)를 만들었는가?

만약 완전한 우변을 만들었을 때, Reduce가 가능함.

• 인식 방법 요약
  • Incomplete RHS : 아직 완성되지 않은 경우이기 때문에 아직 Reduce가 불가능함.
  • Eventually Reduce : 계속 Shift를 하다보면 결국 Reduce를 할 수 있음.
  • 한 개 이상이면 일단 Shift : RHS가 완성되지 않으면 계속 Shift 하는게 원칙 이라는 뜻
• Viable Prefix 요약

1. Shift-Reduce Parsing 에서 Stack에 push 되는 것들이 모두 Viable Prefix이여야 함.
2. 이 개념을 바탕으로 파싱 상태(state)를 정의하고 DFA를 구성
3. Viable Prefix를 인식하는 DFA가 핸들 인식의 기초

Item

Viable Prefix를 인식하는 방법의 새로운 개념

문법의 production rule에 점 (dot)을 찍어 현재 분석 상태를 나타내는 형태를 말함.

Viable Prefix는 스택에 있는 문자열이 올바른 핸들 앞부분인지를 판단함.

그 판단을 위하여 점(dot)을 사용해 현재 분석 위치를 명시함. 그래서 Item의 집합을 이용해서 Viable Prefix들을 구별하고, shift/reduce 동작을 결정할 수 있음.

Viable Prefix To NFA 인식

Viable Prefix를 인식하는 NFA(비결정적 유한 오토마타)를 만드는 방법

1. 새로운 시작 규칙 추가

S' → S

• 기존의 시작 심볼 S를 새로운 시자 심볼 S’로 바꿔줌.
• 모든 파싱의 시작은 이 S’ 에서 시작함.

1. NFA의 구성요소

• States : CFG에서 G에서 모든 items (시작 규칙도 포함)
• Alphabet : G에 등장하는 모든 기호들
• Start State : 시작 규칙
• 모든 State는 accept state : (Viable Prefix는 어느 지점에서도 유효하기 때문)

1. Transition 만들기

예시 )

From: E → α • X β
To: E → α X • β
On: input X

3-1 . Transition 만들기 - (ε-move)

• dot 앞의 X가 non-terminal이고, 해당 production이 존재하면, ε-transition으로 새로운 item들을 추가해줌 (Closure 확장)

• NFA -> DFA

  • NFA 상태는 “단일 item”
  • DFA 상태는 ““item들의 closure 집합
  • DFA transition은 dot을 terminal 또는 non-terminal 기호 뒤로 옮긴 결과
  • 이동한 item으로부터 다시 closure 수행

위 과정을 반복하면 결과적으로

• DFA = LR(0) Automation
• 각 상태 = 여러 item들의 모음
• Transition = dot 오른쪽 심볼을 기준

이 과정까지 끝냈으면, 우리는 Viable prefix 를 활용해 bottom-up parsing 을 가능하다.

LR(0) Parsing

• Reduce, if there is a handle
• Shift, if we still get viable prefix after shifting
• Otherwise, reject

LR Parsing에서는 충돌 발생 가능성이 아직 존재한다. 그래서 predicton을 위한 1개의 token을 추가한 SLR(1) 파싱을 사용하면 충돌 해결이 가능하다.

---

SLR(1) Parsing

LR(0)의 Reduce 조건

• 항목이 A -> a. 처럼 완료된 상태라면, 입력 기호가 무엇이든지 간에 Reduce를 진행함.

• 따라서 문맥을 전혀 고려하지 못해 Shift/Reduce, Reduce/Reduce Conflict들이 자주 발생함.

SLR(1) Parsing에는 LR(0) Parsing에 하나의 조건이 더 추가된다.

항목이 A → α •이면, 현재 입력 기호가 Follow(A)에 있을 때만 Reduce A → α 수행

• 즉, 입력 기호를 조건으로 추가함으로써 conflict를 줄일 수 있다.

SLR Parsing Table 만들기

전체 : 필요한 준비

• CFG(문맥 자유 문법)
• Augmented Grammar (S' -> S) 생성이 되어있는 DFA와 LR(0) 항목

1. Shift 액션 추가 (ACTION 테이블)

• ACTION[i, a] = shift j
  • a는 터미널 기호이고, a에 대한 전이로 j state에 가게 될 때 사용
  • 예시) S5와 같이 몇 번 state로 가라고 작성

2. Reduce 액션 추가 (ACTION 테이블)

• ACTION[i, a] = reduce A → α
  • 상태 i에 완료된 항목이 있고,
  • a ∈ FOLLOW(A) 일 때, R4와 같이 사용

여기서 R 뒤에 적은 숫자는 CFG의 문법 번호를 작성해야함.

FOLLOW 집합을 사용한다는 점이 SLR(1) 의 핵심

3. GOTO 테이블 생성

• GOTO[i, B] = j
  • 상태 i에서 non terminal B에 대해 전이된 상태가 j 일 때 사용
  • 단순하게, Non-terminal에 몇번의 state로 가는지 작성해주기

4. Accept 액션 지정

• ACTION[i, $] = accept
  • 상태 i에 S'-> S. 항목이 있을 때, 입력 기호가 $
  • 문맥을 읽었다. (수락했다) 라고 지정해주는 마지막 표시

5. 오류 처리(공백은 에러)

• ACTION, GOTO 테이블에 정의되지 않은 항목은 에러 상태로 간주한다.

다음은 SLR(1) Parser Table의 예시이다.

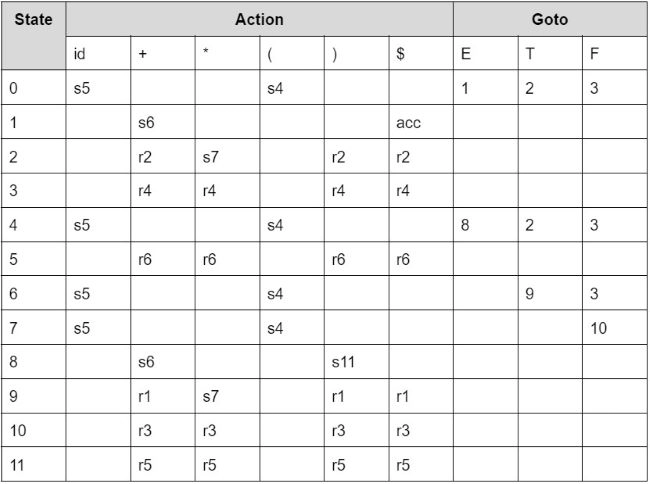
다음은 SLR table에 stack을 사용한 간단한 알고리즘이다.

def slr_parse(input_tokens, action_table, goto_table, productions):
    stack = [0]
    input_tokens.append('$')
    pointer = 0

    while True:
        state = stack[-1]
        current_token = input_tokens[pointer]
        
        action = action_table.get((state, current_token))

        if action is None:
            print("Parsing error!")
            return False

        if action[0] == 'shift':
            stack.append(current_token)
            stack.append(action[1])
            pointer += 1

        elif action[0] == 'reduce':
            lhs, rhs = productions[action[1]]
            pop_len = 2 * len(rhs)
            stack = stack[:-pop_len]
            state = stack[-1]
            stack.append(lhs)
            stack.append(goto_table[(state, lhs)])

            print(f"Reduce by {lhs} → {' '.join(rhs) if rhs else 'ε'}")

        elif action[0] == 'accept':
            print("Input accepted!")
            return True

CFG Requirements 요약

항목	LL(1) Parsing	SLR(1) Parsing
Ambiguity	허용 안 됨 (non-ambiguous 해야 함)	허용 안 됨 (non-ambiguous 해야 함)
Left Recursion	없어야 함	있어도 됨
Left Factoring	필요함	필요 없음
기타	문법을 단순화해야 함	파싱 테이블에서 모든 ACTION 셀에 충돌이 없어야 함 (deterministic해야 함)

---

AST Construction

AST(Abstract Syntax Tree)

• 프로그래밍 언어나 수식 등의 문법 구조를 트리 형태로 단순화하여 표현한 구조
  • 추상 (Abstract) : 실제 코드의 구체적인 문법 표현을 생략하고 의미적으로 중요한 정보만 담는 트리

  • parser의 단계의 결과로 생성되며, 이후 semantic Analysis 나 코드 생성 단계에서 사용

    		 <=>
     		  /   \
    

    <*> / \ <60>

sntax analysis에서 좋은 output은 무엇인가?

1. 구문 분석 후에는 의미 분석이 이어진다.

• 의미 분석을 위해서는 구문적으로 중요한 정보가 필요하다.

1. 좋은 구문 분석 결과물인 (AST)의 조건

• 중요한 문법 구조를 포함해야한다.
• 효율적이고 단순해야한다.

Parse Tree vs Abstract Syntax Tree

Parse Tree

• 문법 규칙 중 구체 문법에 따른 완전한 트리
• 문법적인 모든 요소를 포함한다. (e.g. 괄호, 중간 노드 등)

AST

• 의미 분석, 코드 생성에 불필요한 노드 제거
• 보다 간결한 표현 -> 이후 컴파일러 단계에 유리

AST 에서 생략 가능한 노드

AST는 간결하고 의미 중심적인 트리를 만들기 위해, 불필요한 구문 정보를 생략한다.

• 단일 자식만 가진 노드 ( Single-successor nodes)
  • 예시 ) Expression → Term → Factor → Identifier
  • 한쪽으로만 계속 이어지는 중간 노드들은 정보 추가 없이 연결만 하기에 생략이 가능하다.
• 구문적 정보 표현용 심볼 (Symbols for describing syntactic details)
  • 예시 ) (), ,,';등
  • 이런 기호들은 문법적으로 문장을 구분하거나 우선순위를 지정하는 용도이기에 의미분석에는 중요하지 않다.
  • 연산자 우선순위만 제대로 표현이 가능하면 괄호 노드는 생략이 가능하다
• 연산자와 피연산자를 자식으로 갖는 중간 논터미널 노드 (Non-terminal)
  • 예시 ) Expression → Expression + Term
  • non-terminal 중에 단순히 연산을 위한 중간 포맷일 경우 생략 가능
  • 중간 비단말이 연산자와 피연산자의 관계를 명확히 나타내지 않고, 단순히 연결만 한다면 의미적으로 쓸모가 없다.

AST Construction

Semantic Action : 각 CFG 규치게 따라 실행되는 작은 코드 조각

• 이는 syntax와 semantics를 연결해주는 다리 역할을 수행한다.
• 예시

Production	Semantic Action	설명
E → T	E.node = T.node	E는 T와 동일한 의미를 갖기 때문에 노드 복사
T → F	T.node = F.node	T는 F와 동일
F → (E)	F.node = E.node	괄호는 생략 가능, 내부 E의 노드만 유지
E → E + T	E.node = new Node(‘+’, E.node, T.node)	+ 연산 AST 노드 생성
T → T * F	T.node = new Node(‘*’, T.node, F.node)	* 연산 AST 노드 생성
F → id	F.node = new Leaf(id, id.value)	리프 노드 생성

      *
     / \
   "x"  +
        / \
      "y" "z"