6 분 소요

이번 포스트에는 Source Coding, Channel Coding과 Modulation에 대해 다룰 예정이다.

Source Coding vs Channel Coding

Coding Theory

  • 데이터를 효율적이고 안전하게 전송하거나 저장하기 위해 코드를 설계하는 이론
  • 두 가지의 목적
    • Data Compression (Source Coding) : 효율성
    • Error Correction (Channel Coding) : 신뢰성

실제 통신 시스템에서는 둘 다 함께 사용함.

간단히 비교를 해보자면,

Source Coding

  • 불필요한 중복 (redundancy)를 제거해서 데이터를 압축한다.
  • 즉, 전송하거나 저장할 데이터량을 줄이는 것이 핵심이다. (ex) Zip 파일, MP3 파일
  • 정보 자체는 손실 없이 보존해야 함.

Channel Coding

  • 전송 도중에 발생하는 오류를 검출하거나 복원할 수 있도록 데이터를 부호화한다.
  • 전송 신뢰성을 확보한다. (오류 정정, 신뢰성, 추가 정보 삽입)
  • 전송 중에 오류 발생을 대비해서 여분의 비트를 추가함.

Source Coding

  • 중복된 정보를 제거해서 데이터를 더 짧고 효율적으로 표현하려는 것
  • 전송해야 할 평균 비트 수를 줄이는 것
  • 정보를 잃지 않고 (= lossless) 비트 수만 줄이는 압축 방식이다.

Introduction

소스 기호

  • 송신하려는 정보는 여러 기호로 구성되어 있음. 예) 알파벳, 숫자, 음성 등 \(S = \{ s_0, s_1, …, s_k \}\)

  • 그리고 각 기호는 고유한 확률로 나타난다. \(\{ p_0, p_1, …, p_k \}\)

각 기호마다 부여된 코드의 길이를 l이라고 한다면, 평균 코드 길이의 수식은 다음과 같다. \(\bar{L} = \sum_{k=0}^K p_k l_k\)

즉, 자주 나타나는 짧은 코드로 드물게 나타나는 기호는 긴 코드로 만드는게 유리하다.

Code Efficiency

만약 이론적으로 가능한 최소 평균길이가 있다면, 코딩 효율은 다음과 같이 정의된다. \(\eta = \frac{L_{\min}}{\bar{L}}\) 1에 가까울수록 이론적으로 최적값에 가까운 효율적인 압축을 의미한다.

Data Compaction

다음 3가지는 압축할 때 만족해야하는 조건이다.

(1) Removal of Redundant : 의미 없는 중복 제거로 비트 수를 감소함.

(2) Loseless data : 정보 손실이 없이 압축해야함.

(3) Uniquely Decodable : 어떤 순서로 코드를 받더라도 원래 메시지를 정확히 복원할 수 있어야함.

Prefix Coding

  • Prefix Code는 가변 길이 부호중에서 특별한 규칙을 따른다.
  • 디코딩이 간단해지기 때문에 사용함.
    • 왼쪽부터 읽으면서 여기까지가 하나의 코드라는 것을 즉시 판단이 가능함.

어떤 코드워드도 다른 코드워드의 접두어(prefix)가 되면 안된다.

  • 특징
    • No prefix rule : 각 코드워드가 다른 코드워드의 시작 부분과 겹치지 않는다.
    • Uniquely decodable : 전송된 비트열을 유일하게 해석할 수 있다.
    • 모든 uniquely decodable code가 prefix가 아니다. : 역은 성립 X

Prefix code 이면서 uniquely decodable 하면 Decision Tree를 만들 수 있다.

즉, 디코딩이 순차적으로 확실히 구분이 가능하다.

수식적 정의

  • 평균 코드 길이 L \(\bar{L} = \sum_{k=0}^{K-1} p_k \cdot l_k\)

    • p : 기호의 등장 확률
    • l : 각 기호의 부여된 비트 수

  • 수학적 조건 (Prefix Code가 되기 위한 조건) \(\sum_{k=0}^{K-1} 2^{-l_k} \leq 1\)

    • 평등일 경우 : 완전한 prefix code
    • 위배되는 경우 : prefix code가 아님.

Huffman Coding

  • 가장 효율적인 무손실 압축 방식 중 하나
  • 각 심볼의 출현 확률에 따라 가변 길이의 코드를 생성하여 Prefix Code를 만든다.

알고리즘 단계

Step 1. Symbol 확률 정렬

  • 심볼들을 출현 확률이 높은 순서대로 정렬하고, 이를 트리의 leaf node로 간주한다.

Step 2. 반복 병합

  • 가장 낮은 두 개의 확률 노드를 선택하여 하나는 0, 다른 하나는 1을 부여한다.
  • 두 개의 노드를 합쳐서 새로운 내부 노드를 만든다. (그 확률은 두 노드의 합)
  • 노드가 하나가 남을 때까지 앞의 두 개의 과정을 반복한다.

Step 3. 코드 부여

  • 각 leaf node부터 루트까지 올라가면서 부여된 비트를 따라간다.
  • 루트까지의 경로가 해당 심볼의 Code word가 된다.

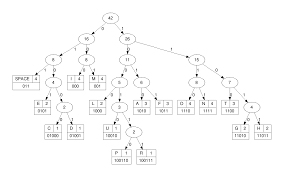
huffman coding

Huffman Coding 특징

  1. 어떤 코드도 다른 코드의 접두어가 아닌 Prefix Code이다. 따라서 즉시 디코딩이 가능하다
  2. 각 심볼에 대한 codeword의 길이는 information 과 같다.
  3. 출현 빈도가 높은 심볼은 짧은 코드를, 출현 빈도가 낮은 심볼은 긴 코드를 가진다.
  4. 확률을 정확히 알고 있을 때, 유용하다.
    • 분산이 클수록 좋다.

Channel Coding

  • 전송 중 발생하는 에러를 검출 및 정정하기 위해 중복비트(redundant bits)를 추가
  • 송신자가 재전송하지 않고도 수신자가 복구가 가능하다.

Forward Error Correction (FEC)

  • 오류가 발생하더라도 수신 측이 재전송 요청 없이 데이터를 복원할 수 있는 기술
  • 추가적인 오류 정정 코드를 함께 전송하고, 수신측은 이 코드를 이용해 오류를 탐지하고 정정한다.

1. Block Codes

  • 정보 데이터를 고정 길이 k비트 블록으로 나눈 뒤, r bit의 parity bit를 추가하여 전체 n bit 의 코드워드로 만들어 전송하는 방식이다.
    • Decoder는 code vector와 error vector의 합으로 본다.
  • k : 원래의 정보 비트 개수
  • r : 추가된 parity 비트 개수
  • n = k + r : 전체 코드워드 길이
  • Code Rate : k/n (정보 비트 비율) -> 코드의 효율성 지표

2. Convolutional Codes

  • 정보를 블록 단위가 아닌 연속적인 비트 스트림으로 인코딩하는 방식의 오류 정정 코드
  • 입력 비트가 순차적으로 들어올 때마다 출력 비트가 생성되고, 현재 입력 비트 뿐만 아니라 이전 입력 비트들도 영향을 준다.
  • ( (n, k, m) ): 출력 비트 수, 입력 비트 수, 메모리 길이
  • 즉 메모리를 갖는 코드

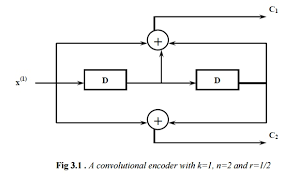
convolutonal code

인코딩 방식 요약

  1. 입력 비트가 순차적으로 들어간다.
  2. 내부 상태는 이전 입력값들을 기억한다.
  3. 매 입력마다 현재 입력과 메모리 값들을 조합해 출력 비트를 2개 생성한다.
  4. 시간이 지남에 따라 누적되듯이 인코딩된다.

3. Interleaving

  • 전송 중 연속적인 오류(Burst Error)가 발생할 경우, 에러가 퍼지도록 데이터를 재배열하여 오류 정정 성능을 높이는 기법
  • 즉, 원래 순서의 데이터를 분산시켜 전송하고 수신 후에 다시 원래 순서로 복원한다.
  • 필요한 이유
    • 대부분의 채널은 burst error를 발생시킨다.
    • 예) 01111100 -> 01xxxxx00 (x : 에러 발생)
    • 일반적인 오류 정정 코드는 흩어진 오류에는 강하지만, 연속된 에러에는 약하다
    • 따라서 에러를 흩어놓기 위해 사용한다.
  • 가로 방향으로 Write, 세로 방향으로 Read를 수행한다.

Shannon Limit

Information Capacity Theorm (Shannon Limit)

  • Shannon 이 제안한 정보 이론의 핵심 정리로, 노이즈가 있는 채널에서 최대 얼마만큼의 정보를 오류 없이 전송할 수 있는지를 수학적으로 정의한 것

  • 수식 \(C = B \log_2\left(1 + \frac{S}{N}\right) \quad \text{[bps]}\)

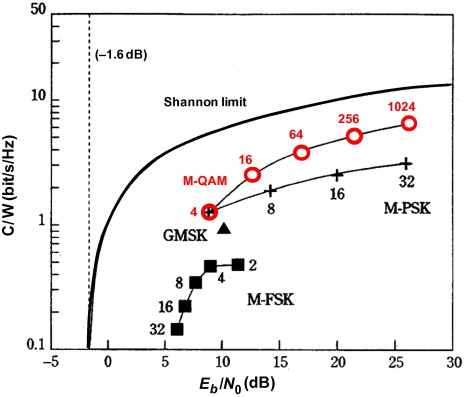
shannon limit

  • 이론적으로는 이 한계치 이하에서는 완벽하게 오류 없는 전송이 가능하다고 증명되었다.
  • 이보다 높은 전송률을 시도하면 어떤 코딩을 사용해도 오류 발생을 피할 수가 없다.

채널 용량이 절대적 한계

  • 아무리 좋은 인코딩 / 디코딩을 해도 Shannon Limit을 넘을 수는 없다.
  • 효율적 통신 시스템 설계의 기준선

Turbo Codes

  • Shannon Limit 한계에 근접한 오류 정정 성능을 가진 FEC 방식
  • 두 개의 convolutional Encoder, Interleaver 를 가진다.
    • Convolutional Encoder : 동일한 구조를 가지고, 하나는 원본 입력 데이터를 사용하고 다른 하나는 Interleaver를 통해 순서를 섞은 입력 데이터를 사용한다.
    • Interleaver : 입력 비트의 순서를 무작위로 재배열하여, 두번째 인코더에 다양한 형태의 입력을 제공하여 오류 정정 성능을 향상한다.

Modulation

  • 디지털 또는 아날로그 신호를 전송 가능한 형태로 변환하는 과정
  • 주로 baseband 신호를 bandpass로 변환하여 전송한다.
    • 저주파 데이터 신호 -> 고주파 전송 신호
  • 전송 매체에 맞는 형태로 바꾸는 것이 변조
  • 필요한 이유
    • 장거리 전송 가능, 안정적인 전송, 다중화 기능

Modulation & Demodulation

변조 (Modulation) : 송신 측에서 수행한다.

  • 정보 신호를 -> 반송파 (Carrier)에 실어서 전송한다.

복조 (Demodulation) : 수신 측에서 수행한다.

  • 반송파 -> 원래 정보 신호로 복원한다.

Demodulation의 역할

  • 수신한 신호를 샘플링하고, 노이지를 제거한 이후에 심볼을 판별하여 원래 비트로 복원한다.

주요 오류 원인

1. AWGN (Additive White Guassian Noise)

  • 열잡음 등으로 인한 추가적인 신호 간섭

2. ISI (Inter-Symbol Interference)

  • 채널의 필터링 효과로 인해 기호 간 관계가 흐려지는 현상
  • 송신기, 수신기, 채널의 영향

Modulation 종류

아날로그 변조 (Analog Modulation)

1. AM (Amplitude Modulation)

  • 반송파의 진폭을 조절하여 정보 전달

2. FM (Frequency Modulation)

  • 반송파의 주파수를 조절

3. PM (Phase Modulation)

  • 반송파의 위상을 조절

디지털 변조 (Digital Modulation)

1. FSK (Frequency Shift Keying)

  • 디지털 0 /1 에 따라 서로 다른 주파수를 사용

2. PSK (Phase Shift Keying)

  • 디지털 값에 따라 위상을 변경한다.

3. QAM (Quadrautre Amplitude Modulation)

  • 진폭과 위상의 조합으로 다중 비트를 전송

Signal Space

Signal Space Concept

  • 각 신호를 N차원의 벡터 공간에서 하나의 벡터로 표현한다.

  • 이 공간을 통해 신호가 에너지, 거리를 계산할 수 있고, 복조 성능을 평가할 수 있다.

  • 벡터 간의 거리가 클수록 서로 구별하기 쉽다 -> 오류의 확률이 낮아진다.

  • 요소들

    • 기저 함수 (Basis Function)

      • 신호 공간을 구성하는 서로 직교한 함수 집합 \(\psi_1(t), \psi_2(t), …, \psi_N(t)\)

      • 어떤 신호도 이들 함수들의 선형 조합으로 표현이 가능하다.

    • 벡터 표현

      • 내적 \(\langle x(t), y(t) \rangle = \int x(t) y^*(t) dt\)

        \[직교 조건: \langle \psi_i(t), \psi_j(t) \rangle = 0 (i ≠ j)\]

  • 신호 에너지 \(E = \int |s(t)|^2 dt = \|\mathbf{s}\|^2\)

    • 유클리드 거리 (신호 간 거리) \(d(s_1, s_2) = \|\mathbf{s}_1 - \mathbf{s}_2\|\)

Orthogonal Signal Space

  • 서로 직교하는(N개) 기저 함수들을 사용해 신호를 벡터로 표현하는 공간

  • 각 신호를 직교 벡터 조합으로 표현함으로써, 신호 간 구분과 복조를 수학적으로 처리가 가능하다. \(\langle \psi_i(t), \psi_j(t) \rangle = \int_0^T \psi_i(t) \psi_j^*(t) dt = 0 \quad (i \ne j)\)

    • 위 조건을 만족하고, 각 함수의 에너지가 1일 때 \(\langle \psi_i(t), \psi_i(t) \rangle = 1\)

  • Orthogonal Signal Space의 특징

    • 선형 독립 : 각 기저 함수는 나머지로 표현될 수 없다.
    • 차원 수 N : 서로 다른 N 개의 기저 함수가 필요하다.
    • 신호 표현 : 임의의 신호는 이 기저함수들의 선형결합으로 표현된다.
    • 계산 단순화 : 거리 계산, 에너지 계산이 벡터 공간처럼 단순해진다.

BPSK (Binary Phase Shift Keying)

  • 2개의 위상 상태만 사용하는 가장 간단한 PSK 방식
  • 한 번에 1 bit 전송
  • 진폭만 반전되고 위상은 180도 차이가 난다.
  • 1차원 벡터 공간

QPSK (Quadrature Phase Shift Keying)

  • BPSK 보다 확장된 방식으로, 한 번에 2 bit 전송
  • 4개의 위상 상태를 사용한다.
  • 2차원 공간

BPSK : 단순한고 견고해서 잡음이 심한 환경에서 적합

QPSK : 더 많은 비트를 전송할 수 있어서 대역폭 절약에 효과적

참고

Concurrency, Locks

8 분 소요

이번 포스트는 OS의 Concurrency와 Locks에 대해 다룬다.